Come meccanismo di trasmissione, l'ingranaggio epicicloidale è ampiamente utilizzato in varie applicazioni ingegneristiche, come riduttori, gru, riduttori epicicloidali, ecc. Per i riduttori epicicloidali, può sostituire il meccanismo di trasmissione di un treno di ingranaggi ad asse fisso in molti casi. Poiché il processo di trasmissione degli ingranaggi avviene tramite contatto lineare, un accoppiamento prolungato può causare guasti agli ingranaggi, quindi è necessario simularne la resistenza. Li Hongli et al. hanno utilizzato il metodo di accoppiamento automatico per l'accoppiamento dell'ingranaggio epicicloidale e hanno ottenuto che la coppia e la sollecitazione massima sono lineari. Anche Wang Yanjun et al. hanno accoppiato l'ingranaggio epicicloidale tramite il metodo di generazione automatica e hanno simulato la statica e la simulazione modale dell'ingranaggio epicicloidale. In questo articolo, gli elementi tetraedrici ed esaedrici vengono utilizzati principalmente per suddividere l'accoppiamento e i risultati finali vengono analizzati per verificare se le condizioni di resistenza sono soddisfatte.

1、 Definizione del modello e analisi dei risultati

Modellazione tridimensionale dell'ingranaggio planetario

Ingranaggio planetarioè composto principalmente da corona dentata, ingranaggio solare e ingranaggio planetario. I parametri principali selezionati in questo articolo sono: il numero di denti della corona dentata interna è 66, il numero di denti dell'ingranaggio solare è 36, il numero di denti dell'ingranaggio planetario è 15, il diametro esterno della corona dentata interna è 150 mm, il modulo è 2 mm, l'angolo di pressione è 20°, la larghezza del dente è 20 mm, il coefficiente di altezza dell'addendum è 1, il coefficiente di gioco è 0,25 e sono presenti tre ingranaggi planetari.

Analisi di simulazione statica dell'ingranaggio planetario

Definire le proprietà del materiale: importare il sistema di ingranaggi planetari tridimensionale disegnato nel software UG in ANSYS e impostare i parametri del materiale, come mostrato nella Tabella 1 sottostante:

Meshing: la mesh degli elementi finiti è divisa in tetraedro ed esaedro e la dimensione di base dell'elemento è 5 mm. Poichéingranaggio planetario, l'ingranaggio solare e l'ingranaggio interno sono in contatto e ingranano, la mesh delle parti in contatto e ingranamento viene densificata e la dimensione è di 2 mm. Innanzitutto, vengono utilizzate griglie tetraedriche, come mostrato in Figura 1. In totale vengono generati 105906 elementi e 177893 nodi. Successivamente, viene adottata una griglia esaedrica, come mostrato in Figura 2, e in totale vengono generati 26957 celle e 140560 nodi.

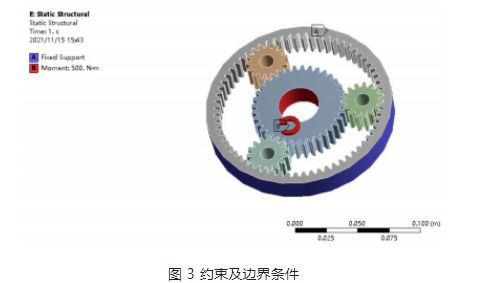
Applicazione del carico e condizioni al contorno: in base alle caratteristiche di funzionamento dell'ingranaggio planetario nel riduttore, l'ingranaggio solare è l'ingranaggio conduttore, l'ingranaggio planetario è l'ingranaggio condotto e l'uscita finale avviene tramite il portasatelliti. Fissare la corona dentata interna in ANSYS e applicare una coppia di 500 N·m all'ingranaggio solare, come mostrato in Figura 3.

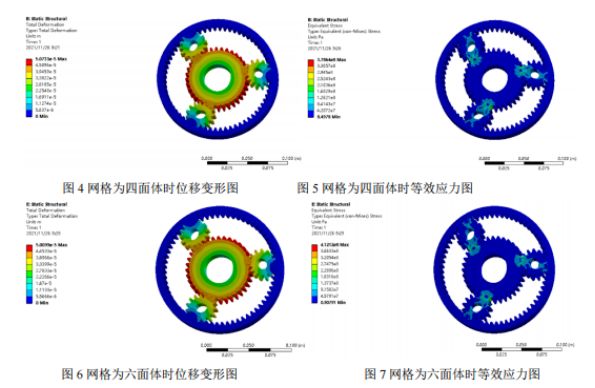
Post-elaborazione e analisi dei risultati: Di ​​seguito sono riportati il ​​nefogramma di spostamento e il nefogramma di sforzo equivalente dell'analisi statica ottenuti da due divisioni della griglia, e viene condotta un'analisi comparativa. Dal nefogramma di spostamento dei due tipi di griglia, si riscontra che lo spostamento massimo si verifica nella posizione in cui l'ingranaggio solare non innesta con l'ingranaggio planetario e lo sforzo massimo si verifica alla radice dell'ingranamento. Lo sforzo massimo della griglia tetraedrica è di 378 MPa e lo sforzo massimo della griglia esaedrica è di 412 MPa. Poiché il limite di snervamento del materiale è di 785 MPa e il fattore di sicurezza è 1,5, lo sforzo ammissibile è di 523 MPa. Lo sforzo massimo di entrambi i risultati è inferiore allo sforzo ammissibile ed entrambi soddisfano le condizioni di resistenza.

2、 Conclusion

Attraverso la simulazione agli elementi finiti dell'ingranaggio planetario, si ottengono il nefogramma di deformazione dello spostamento e il nefogramma di sforzo equivalente del sistema di ingranaggi, da cui si ricavano i dati massimi e minimi e la loro distribuzione nelingranaggio planetarioÈ possibile trovare un modello. La posizione della massima sollecitazione equivalente è anche quella in cui è più probabile che i denti dell'ingranaggio si rompano, pertanto è necessario prestare particolare attenzione a questo aspetto durante la progettazione o la produzione. Attraverso l'analisi dell'intero sistema di ingranaggi planetari, l'errore causato dall'analisi di un solo dente dell'ingranaggio viene superato.